انتگرال گیری عددی

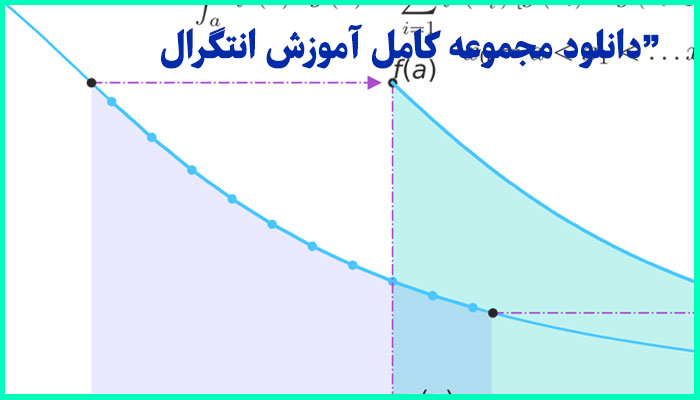
شکل ۱: تقریب مساحت با مستطیل‌ها و ذوزنقه‌ها انتگرال عددی با قاعده ذوزنقه‌ای برای استفاده از این روش، بازه انتگرال‌گیری را به n n زیربازه به طول Δx Δ x تقسیم می‌کنیم. یک ذوزنقه معمولی در شکل ۲ نشان داده شده که مساحت آن برابر با f (xi)+f (xi+1) 2 Δx f ( x i) + f ( x i + 1) 2 Δ x است. اگر مساحت کل ذوزنقه‌ها را با یکدیگر جمع کنیم، خواهیم داشت:
انتگرال عددی تقریب عددی مساحت S {\displaystyle S} است. انتگرال عددی ( انگلیسی: Numerical integration) یا ادغام عددی و یکپارچه سازی عددی در آنالیز عددی است، انتگرال گیری عددی به منزله یک خانواده گسترده‌ای از ...
انتگرال‌گیری در واقع برعکس مشتق‌گیری است و برای محاسبه مقدار یک تابع در یک بازه مشخص از محور مستقل به کار می‌رود. اهمیت یادگیری مشتق‌گیری و انتگرال‌گیری عددی چیست؟ یکی از درس‌های خیلی جذاب در مقطع کارشناسی اکثر رشته‌های مهندسی، درس محاسبات عددی است که اغلب در ترم‌های دوم یا سوم ارائه می‌شود.

توجه: لطفا پیش از خرید هر محصول، روی دکمه جزئیات کلیک کنید و توضیحات را مطالعه کنید.